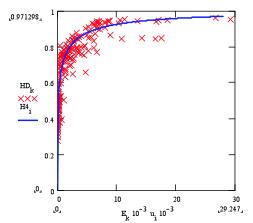
The United Nations uses an economic parameter called the Human Development Index (HDI) to characterize the typical standard of living of every nation. It is observed that affluent nations have high HDI scores (they range from 0 to 1) and a high use of electrical energy per year per capita (in kilowatt-hours/year/person the range is from 0 to 30,000), while poor nations have relatively low values for both quantities. The following graph shows 2005 data for 177 nations (red x), and a curve fitted to the trend of the data (blue line); HDI is plotted along the vertical axis, energy use (MW-hr/year/person) is plotted along the horizontal axis.
Data from 2005 include the following:
1. The range of annual per capita electrical energy use among 177 nations was between 40 kWh/year/person and 29,247 kWh/year/person. The range of HDI was 0.281 to 0.963.
2. The United States of America ranked 10th in HDI, at 0.944, with 13,456 kWh/y/p for 4.5% of the world’s population, which produced 24.4% of the CO2 emissions from human activity.
3. The People’s Republic of China ranked 85th in HDI, at 0.755, with 1,484 kWh/y/p for 21% of the world’s population, which produced 12.1% of the CO2 emissions from human activity.
How are the Human Development Index (HDI) and per capita electrical energy use related quantitatively? How are the energy technologies chosen to power a nation or region related to the political economy there?
I explored these questions in 2006, and wrote several reports that present my findings. It is my belief that the United States has wasted the years since 1973 — the first Arab Oil embargo — by not developing a robust public energy generation network for the nation, to replace the patchwork of private fossil fuel and and nuclear energy powered grids we still have today.
Hence, my EFHD reports #1 (Energy for Human Development) and #2 (The Circle of Power) remain up to date. Here they are:
My “GNEP” series of reports is summed up in a presentation (Energy Choices For An Uncertain Future) on the use of Decision Theory to show how the character or preferences of the national persona (or that group empowered to choose the energy technologies for the nation) can be quantified and used to rank the choices between all the combinations of: renewables, coal, nuclear and oil.
Graphs of the correlation between HDI and per capita electrical energy use are presented in this next report (Comparing HDI and Energy Use, Data & Model)
The way that Decision Theory was used to rank energy choices is described at length in the next report (Ranking Energy Choices For An Uncertain Future)
Technology is not the barrier.
Enjoy

The Economy Is Not Coming Back, Part III: The Reasons it Shouldn’t
by Gilles d’Aymery (15 November 2010)
http://www.swans.com/library/art16/ga290.html
“But, more importantly, profound and intensifying environmental and ecological crises militate in favor of not having the economy revert to the shape and form it had. Some of these crises are the object of this third part. In short, to return to business as usual will lead to collective suicide, which Mother Nature will trigger in the not so distant future.”
Pingback: The Economic Function Of Energy | manuelgarciajr
“Energy For Human Development,” EFHD Report #1 (2006) is used in the Asia Development Bank’s 2007 book “Energy for All: Addressing the Energy, Environment, and Poverty Nexus in Asia.”
http://beta.adb.org/publications/energy-all-addressing-energy-environment-and-poverty-nexus-asia
The book is available as a free PDF file. The hyperbolic tangent HDI model from EFHD Report #1 is used in part 2 of the ADB book (“Energy, The Common Denominator,” figures 32, 33). The ADB’s discussion of the movement in the HDI-energy plane by selected lower HDI Asian countries, from 1995 to 2002, is interesting and shows how the HDI-energy model (curve) helps one interpret national trends.
A more recent summary of my work on “energy for human development,” including numerical examples of hypothetical “energy futures” for North America, and as comprehensive a scope as I could manage, is:
The Economic Function Of Energy
27 February 2012
http://www.swans.com/library/art18/mgarci41.html
This article is my best effort toward a theory of ecologically sustainable industrialization, that is to say the use of (exosomatic) energy by human society.
I hope some young engineers and mechanics out there pick up on the suggestions made here, and make clever uses of solar (and wind and water) energy, and applications of thermodynamics, heat transfer and thermal diffusivity, which are both technically simple (which means they may be very intellectually challenging to devise — but isn’t this a joy for engineers?) and make significant improvements to the conditions of human survival for those at the bottom of the energy ladder and HDI scale.
The “development” in my phrase “energy for human development” is only secondarily in reference to economic and infrastructure expansion; it is primarily in reference to the expansion of the freedom of individuals to develop themselves intellectually and socially because of their greater access to energy from ecologically clean sources, which would be applied to easing (removing?) the burdensome chores of survival.
My report EFHD_R_01, cited at the beginning of the article above,
An Introduction Linking Energy Use And Human Development
28 April 2006
has been used by a number of authors since it first appeared on the Internet (in HTML format, in Microsoft’s “htm” version) at http://www.idiom.com/~garcia/EFHD_01.htm [now a legacy web site].
A recent example, with extensive use of my text (EFHD_R_01 is mentioned at one point), is:
Energy Crisis In Pakistan, (10 November 2012)
by Awaan (Adnan Zafar)
“Awaan” is impassioned, and makes a spirited and probing case for clean government that can expand access to electricity economically and efficiently for the benefit of the large portion of low-HDI Pakistanis.
I’m glad to see my EFHD_R_01 used in this way.
As in previous comment, another use of EFHD_R_01 appears as reference 6 in
Energy Scenarios And Vision 2020 In India
2012 (before November 10)
P. Garg
http://www.scribd.com/doc/109527146/7-Energy-Scenarios-Pp-7-17
I first posted EFHD_R_01 on the Internet on 28 April 2006.
A Google search for the phrase
“energy for human development”
finds the following number of instances within given time intervals:
1 January 1990 – 1 January 2000: 1 (not EFHD_R_01)
1 January 2000 – 1 January 2006: 5 (not EFHD_R_01)
1 January 2006 – 27 April 2006: 0
1 January 2006 – 1 January 2007: 1 (EFHD_R_01 at the idiom/~garcia site)
1 January 2007 – 1 January 2008: 2
1 January 2008 – 1 January 2009: 2
1 January 2009 – 1 January 2010: 13
1 January 2010 – 1 January 2011: 16
1 January 2011 – 1 January 2012: 23 (one is my blog posting of EFHD_R_01)
1 January 2012 – 11 November 2012: 14 (excluding my postings citing EFHD_R_01)
1 January 2006 – 11 November 2012: 69 total (excluding my postings)
IEA World Energy Outlook 2012